原文題目

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

題目摘要

1. 問題描述：給定一個 n x n的二維矩陣，要求將這張圖像順時針旋轉 90 度。必須在原地進行旋轉，不能分配其他的二維矩陣儲存旋轉後的結果。
2. 輸入：一個n x n的整數矩陣matrix，其中n為矩陣的邊長。
3. 輸出：旋轉後的矩陣。

Example 1:

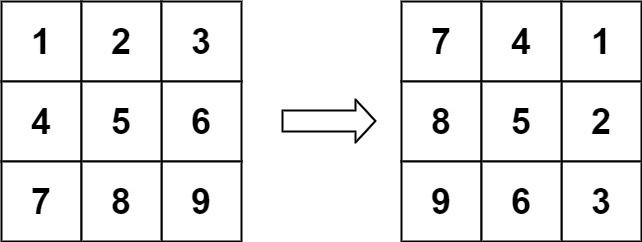
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

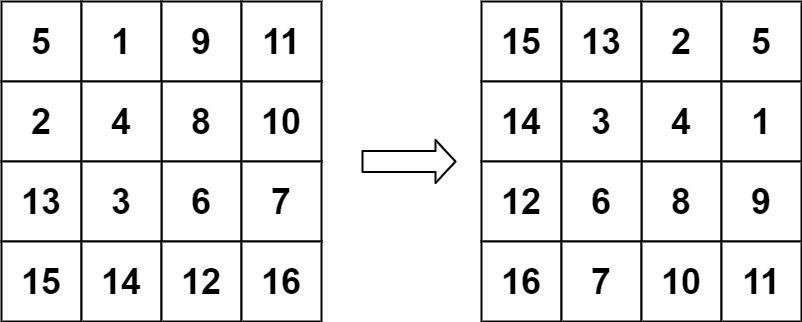
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

解題思路

這題要求我們將矩陣原地旋轉90度，因此不能使用額外的矩陣來幫助解決。可以將問題分為兩個步驟：

1. 矩陣轉置（Transpose）：
   • 先將矩陣沿著對角線翻轉，這樣可以將行變成列。換句話說，將矩陣中的元素matrix[i][j] 交換成matrix[j][i]。
2. 水平翻轉（Horizontal Flip）：
   • 接著，將矩陣的每一行沿著中間線進行翻轉，這樣就完成了順時針90度的旋轉。

程式碼

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        //1. 先進行矩陣轉置
        for (int i=0; i < n; i++) {
            for (int j=i+1; j < n; j++) {  //只處理上三角區域，避免重複交換
                //交換 matrix[i][j]和matrix[j][i]
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        //2. 再進行水平翻轉
        for (int i=0; i < n; i++) {
            for (int j=0; j < n/2; j++) { //只遍歷前半部分的元素
                //交換 matrix[i][j]和matrix[i][n-1-j]
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][n-1-j];
                matrix[i][n-1-j] = temp;
            }
        }
    }
}

結論： 在日常生活中，矩陣的概念可以用來理解許多事物，比如電子表格或遊戲中的棋盤。此題要求將一個二維矩陣順時針旋轉 90 度，而這個過程的挑戰在於不能使用額外的空間。解決這個問題的關鍵在於兩個步驟：先對矩陣進行轉置，再進行水平翻轉。透過這樣的方式，我們能夠在不額外使用空間的情況下，完成矩陣的旋轉，這就像是以巧妙的方式重新排列家裡的家具，讓空間變得更有效率！